Reinforcement Learning Using Rainbow with PyTorch

What Is Reinforcement Learning?

Reinforcement Leaning (RL) is the ability to learn a strategy in a given environment without any supervision. It interacts with an environment, can take actions and see the result where the goal is to gain maximum cumulative score.

Breakout and Pacman Results

I used two Atari games: "Breakout" and "MsPacman" where the computer learned how to play without any prior knowledge and got excellent results:

In the Breakout game, it learns to tunnel the ball at the top to gain maximum score.

In the Pacman game, the goal was to finish the game and not to gain maximum score by eating ghosts.

A (short) Theory

There are many methods for reinforecment learning. The focus here is on the Rainbow method which combines a few algorithms to improve the results and performance.

The problem is defined by an agent interacting with an environment. An environment can be a game, a simulation, a task a robot takes, etc. This example uses the OpenAI Gymnasium package that simulates Atari games.

The Agent observe the state (the pixels of the screen), takes an action (moving the game joystick), and get reward. It repeats this process until the game ends. The goal is to define the strategy the agent should take to gain maximum cumulative rewards (the score of the game).

A Transition is defined as the combination of: $$ (s_t, a_t) \rightarrow (r_{t+1}, s_{t+1}) $$

Which means observe the state in time t, take the action a. This leads to a reward and state at time t+1.

It is assumed that the problem is framed as Markov Decision Process which means that future only depends on the current state and not on the history. The current state itself is based on the history.

The Reward function R predicts the next reward triggered by one action:

$$ R(s,a) = \mathbb{E}[R_{t+1}|S_t = s, A_t = a] = \Sigma_{r}r\Sigma_{s_{t+1}} P(s_{t+1},r|s_t,a) $$

We define the Return function as the discounted sum of reward from time t:

$$ G_t = R_{t+1} + \gamma R_{t+2} + ... = \Sigma_{k=t}^\infty\gamma^{k-t+1}R_{k} $$

The factor gamma is used to penalize future rewards because they are uncertain, they don't provide immediate benefit, and prevent infinite loops.

A Policy $\pi$ is the algoritm to select the best action given a state. The best action maximize the expected value of the future rewards

The Value function is the expected Return for state s:

$$ V_\pi(s) = \mathbb{E}_\pi[G_t|S_t = s] $$

The Q-Function is the expected Return for the state s and action a pair:

$$ Q_\pi(s,a) = \mathbb{E}_\pi[G_t|S_t = s, A_t = a] $$

In a complex environment, we use Deep Neural Network (DNN) to approximate the Q-Function.

We define the Advantage as the differenece between Q-Function and the Value function and it represents the advantage for the given state:

$$ A_\pi(s,a) = Q_\pi(s,a) - V_\pi(s) $$

The optimal policy is the action that gets the maximal return = $ argmax_\pi [Q_\pi(s,a)] $

The Bellman Equations represents the value function as the immediate reward + future values as follows:

$$ \begin{aligned} V(s) &= \mathbb{E}[G_t \vert S_t = s] \\ &= \mathbb{E} [R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots \vert S_t = s] \\ &= \mathbb{E} [R_{t+1} + \gamma (R_{t+2} + \gamma R_{t+3} + \dots) \vert S_t = s] \\ &= \mathbb{E} [R_{t+1} + \gamma G_{t+1} \vert S_t = s] \\ &= \mathbb{E} [R_{t+1} + \gamma V(S_{t+1}) \vert S_t = s] \end{aligned} $$

Similarly for the Q-Function: $$ \begin{aligned} Q(s, a) &= \mathbb{E} [R_{t+1} + \gamma V(S_{t+1}) \mid S_t = s, A_t = a] \\ &= \mathbb{E} [R_{t+1} + \gamma \mathbb{E}_{a\sim\pi} Q(S_{t+1}, a) \mid S_t = s, A_t = a] \end{aligned} $$

DQN Method

A DQN uses deep learning to estimate the Q-Function and take the best action. It uses, Epsilon-Greedy to slowly move between exploration (taking random actions) and explotation (taking actions by the policy). A Replay Memory remembers previous experiences to breaks temporal correlation and biases. It mixes past and recent transitions when training the network. The Q-Function is predicted using an online policy trained with gradient decent. The online policy is copied periodically to a Target Network which is used for future rewards computation. This stabilizes training

Rainbow

The Rainbow scheme combines multiple improvements for DQN:

• Double Q learning - in some cases Q-Learning over estimat action bias, this leads to sub-optimal policies. Double Q-learning decouples the action selection from the target network
• Prioritized replay - selects samples from the replay memory with higher errors more often. These samples has more to learn from
• Duelling network - composed of two streams, the first stream estimates the state value, the second stream estimates the advantage. Both streams are combined to produce the state, action result. Both streams share the same convolutional feature extraction
• Multi-step learning - Looking n-steps into the future to update the Q-function, leads to faster learning
• Distributional reinforcement learning - learning to approximate the distribution of the return instead of the expexted return. This leads to better generalization
• Noisy Nets - Use DNN with additional noise. It replaces the epsilon greedy scheme by adding noise to the network. Over time the network learns to ignore the noisy stream. The amount of noise added to the netowrk is truned during the training and is increasing the efficiency

Code

Imports & Setup

import gymnasium as gym
import matplotlib
import matplotlib.pyplot as plt
from collections import namedtuple, deque
from itertools import count
import imageio
import ipywidgets
import numpy as np
import random
import math
from abc import ABC

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

# set up matplotlib
is_ipython = 'inline' in matplotlib.get_backend()
if is_ipython:
    from IPython import display

# Enable interactive mode
plt.ion()

# if GPU is to be used
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Parameters

game_params = {
    'GAME_ID': "MsPacmanNoFrameskip-v4",
    'SKIP_FRAMES': 4,  # How many frames to skip in the environment
    'FIRE_TO_START': False,  # Click fire to start or when losing life
    'OPT_FRUITS': True  # reward only fruits, not ghost eating
}

# Agent params
params = {
    "lr": 6.25e-5,              # learning rate
    "mem_size": 300000,         # Size of the memory buffer
    "interval": 10,             # how often parameters should be saved and printed
    "do_train": True,           # train or play
    "train_from_scratch": True, # train from scratch or continue from previous tries
    "n_step": 3,                # multi-step reward
    "batch_size": 32,           # training batch size
    "state_shape": (4, 84, 84), # shape of observation state
    "max_steps": int(1e+8),     # max train steps
    "gamma": 0.99,              # gamma reduction of older rewards
    "beta": 0.4,                # initial beta, percentage to use policy vs. random-action
    "train_period": 4,          # frequence to update beta
    "v_min": -10,               # min and max of distribution predictions
    "v_max": 10,
    "n_atoms": 51,              # number of discrete distribution values
    "adam_eps": 1.5e-4,         # Adam optimizer epsilon
    "alpha": 0.5,               # how much prioritization is used (0 - no prioritization, 1 - full prioritization)
    "clip_grad_norm": 10.0,     # gradient cliping
    "final_annealing_beta_steps": int(1e+6),  # when to finish random actions
    "initial_mem_size_to_train": 1000,        # min memory steps to start training
    "seed": 123,                # random seed              
    "tau": 1.25e-4,             # factor for updating online network from target network
    "hard_update_freq": 8000,   # frequency to update network  
    "max_frames_per_episode": int(108e3),  # max episode frame
    "save_n_rewards": 1000,     # number of last rewards to plot
    "avg_window": 50            # average rewards calculation window
}

Environment

class FireResetEnv(gym.Wrapper):
    def __init__(self, env):
        super(FireResetEnv, self).__init__(env)
        assert env.unwrapped.get_action_meanings()[1] == 'FIRE'
        assert len(env.unwrapped.get_action_meanings()) >= 3

    def reset(self):
        self.env.reset()
        obs, _, terminated, truncated, info = self.env.step(1)
        done = terminated or truncated
        if done:
            self.env.reset()
        obs, _, terminated, truncated, info = self.env.step(2)
        done = terminated or truncated
        if done:
            self.env.reset()
        return obs, info

env = gym.make(game_params['GAME_ID'], render_mode="rgb_array")
# Atari preprocessing wrapper
env = gym.wrappers.AtariPreprocessing(env,
                                      noop_max=30,
                                      frame_skip=game_params['SKIP_FRAMES'],
                                      screen_size=84,
                                      terminal_on_life_loss=False,
                                      grayscale_obs=True,
                                      grayscale_newaxis=False,
                                      scale_obs=False)
# Frame stacking
env = gym.wrappers.FrameStack(env, 4)
if game_params['FIRE_TO_START']: env = FireResetEnv(env)

Replay Buffer

# Taken from https://github.com/alirezakazemipour/Rainbow/tree/master/Memory
class MinSegmentTree:
    def __init__(self, capacity):
        assert capacity > 0 and capacity & (capacity - 1) == 0  # Full binary tree
        self.capacity = capacity
        self.tree = list(np.full(2 * self.capacity, np.inf))

    def query(self, start_idx, end_idx, current_node, first_node, last_node):
        if start_idx == first_node and end_idx == last_node:  # If we're on the node that contains what we want.
            return self.tree[current_node]
        mid_node = (first_node + last_node) // 2
        if mid_node >= end_idx:  # If the range lays completely on the left child
            return self.query(start_idx, end_idx, 2 * current_node, first_node, mid_node)
        elif mid_node + 1 <= start_idx:  # If the range lays completely on the right child
            return self.query(start_idx, end_idx, 2 * current_node + 1, mid_node, last_node)
        else:  # If the range lays partially on the left & right children
            return min(self.query(start_idx, mid_node, 2 * current_node, first_node, mid_node),  # Left part
                       self.query(mid_node + 1, end_idx, 2 * current_node + 1, mid_node + 1, last_node))  # Right part

    def min(self, start_idx=0, end_idx=None):
        if end_idx is None:
            end_idx = self.capacity
        elif end_idx < 0:
            end_idx += self.capacity
        end_idx -= 1
        return self.query(start_idx, end_idx, 1, 0, self.capacity - 1)

    def __setitem__(self, idx, value):
        idx += self.capacity
        self.tree[idx] = value
        # propagate the change through the tree.
        idx //= 2
        while idx >= 1:
            self.tree[idx] = min(self.tree[2 * idx], self.tree[2 * idx + 1])
            idx //= 2

    def __getitem__(self, idx):
        assert 0 <= idx < self.capacity
        idx += self.capacity
        return self.tree[idx]


class SumSegmentTree:
    def __init__(self, capacity):
        assert capacity > 0 and capacity & (capacity - 1) == 0  # Full binary tree
        self.capacity = capacity
        self.tree = list(np.full(2 * self.capacity, 0))

    def query(self, start_idx, end_idx, current_node, first_node, last_node):
        if start_idx == first_node and end_idx == last_node:  # If we're on the node that contains what we want.
            return self.tree[current_node]
        mid_node = (first_node + last_node) // 2
        if mid_node >= end_idx:  # If the range lays completely on the left child
            return self.query(start_idx, end_idx, 2 * current_node, first_node, mid_node)
        elif mid_node + 1 <= start_idx:  # If the range lays completely on the right child
            return self.query(start_idx, end_idx, 2 * current_node + 1, mid_node, last_node)
        else:  # If the range lays partially on the left & right children
            return self.query(start_idx, mid_node, 2 * current_node, first_node, mid_node) + \
                   self.query(mid_node + 1, end_idx, 2 * current_node + 1, mid_node + 1,
                              last_node)  # Left + Right parts

    def sum(self, start_idx=0, end_idx=None):
        if end_idx is None:
            end_idx = self.capacity
        elif end_idx < 0:
            end_idx += self.capacity
        end_idx -= 1
        return self.query(start_idx, end_idx, 1, 0, self.capacity - 1)

    def find_node(self, prior):
        assert 0 <= prior <= self.sum() + 1e-5

        idx = 1  # root
        while idx < self.capacity:
            if self.tree[2 * idx] > prior:  # Left child.
                idx *= 2
            else:
                prior -= self.tree[2 * idx]
                idx = 2 * idx + 1
        return idx - self.capacity

    def __setitem__(self, idx, value):
        idx += self.capacity
        self.tree[idx] = value
        # propagate the change through the tree.
        idx //= 2
        while idx >= 1:
            self.tree[idx] = self.tree[2 * idx] + self.tree[2 * idx + 1]
            idx //= 2

    def __getitem__(self, idx):
        assert 0 <= idx < self.capacity
        idx += self.capacity
        return self.tree[idx]
    
class ReplayMemory:
    def __init__(self, capacity, alpha, seed):
        self.capacity = capacity
        self.max_priority = 1
        self.alpha = alpha
        self.memory = []
        random.seed(seed)

        n_nodes = 1
        while n_nodes < self.capacity:
            n_nodes *= 2
        self.sum_tree = SumSegmentTree(n_nodes)
        self.min_tree = MinSegmentTree(n_nodes)
        self.tree_ptr = 0

    def add(self, *item):
        if len(self.memory) == self.capacity:
            self.memory.pop(self.tree_ptr)

        self.memory.insert(self.tree_ptr, item)
        self.sum_tree[self.tree_ptr] = self.max_priority ** self.alpha
        self.min_tree[self.tree_ptr] = self.max_priority ** self.alpha
        self.tree_ptr = (self.tree_ptr + 1) % self.capacity

        assert len(self.memory) <= self.capacity

    def sample(self, batch_size, beta):
        indices = []
        weights = []
        p_total = self.sum_tree.sum(0, len(self))
        p_min = self.min_tree.min() / p_total
        max_weight = (p_min * len(self)) ** (-beta)
        segment = p_total / batch_size

        for i in range(batch_size):
            a = segment * i
            b = segment * (i + 1)
            upper_prior = random.uniform(a, b)
            idx = self.sum_tree.find_node(upper_prior)
            indices.append(idx)
            sample_prob = self.sum_tree[idx] / p_total
            weights.append((len(self) * sample_prob) ** -beta)
        weights = np.asarray(weights) / max_weight

        return [self.memory[index] for index in indices], weights, np.asarray(indices)

    def update_priorities(self, indices, priors):
        assert len(indices) == len(priors)
        assert (priors > 0).all()
        assert 0 <= indices.all() < self.capacity

        for idx, prior in zip(indices, priors):
            self.sum_tree[idx] = prior ** self.alpha
            self.min_tree[idx] = prior ** self.alpha

        self.max_priority = max(self.max_priority, max(priors))

    def __len__(self):
        return len(self.memory)

Model

class Model(nn.Module, ABC):
    def __init__(self, state_shape, n_actions, n_atoms, support, device):
        super(Model, self).__init__()
        channel = state_shape[0]
        self.n_actions = n_actions
        self.state_shape = state_shape
        self.n_atoms = n_atoms
        self.support = support
        # Input = (4 x 84 x 84)
        self.conv1 = nn.Conv2d(channel, 32, kernel_size=8, stride=4)
        # (84 - 8) / 4 + 1 = 20 => (32 x 20 x 20)
        self.conv2 = nn.Conv2d(32, 64, kernel_size=4, stride=2)
        # (20 - 4) / 2 + 1 = 9 => (64 x 9 x 9)
        self.conv3 = nn.Conv2d(64, 64, kernel_size=3, stride=1)
        # (9 - 3) / 1 + 1 = 7 => (64 x 7 x 7)

        linear_input_size = 7 * 7 * 64  # 3136

        self.adv_fc = NoisyLayer(linear_input_size, 512, device)
        self.adv = NoisyLayer(512, self.n_actions * self.n_atoms, device)

        self.value_fc = NoisyLayer(linear_input_size, 512, device)
        self.value = NoisyLayer(512, self.n_atoms, device)

        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.orthogonal_(m.weight, gain=math.sqrt(2))
                m.bias.data.zero_()

    def forward(self, inputs):
        x = inputs / 255.
        x = F.relu(self.conv1(x))
        x = F.relu(self.conv2(x))
        x = F.relu(self.conv3(x))
        x = x.contiguous()
        x = x.view(x.size(0), -1)

        adv_fc = F.relu(self.adv_fc(x))
        adv = self.adv(adv_fc).view(-1, self.n_actions, self.n_atoms)
        value_fc = F.relu(self.value_fc(x))
        value = self.value(value_fc).view(-1, 1, self.n_atoms)

        mass_probs = value + adv - adv.mean(1, keepdim=True)
        return F.softmax(mass_probs, dim=-1)

    def get_q_value(self, x):
        dist = self(x)
        q_value = (dist * self.support).sum(-1)
        return q_value

    def reset(self):
        self.adv_fc.reset_noise()
        self.adv.reset_noise()
        self.value_fc.reset_noise()
        self.value.reset_noise()


class NoisyLayer(nn.Module, ABC):
    def __init__(self, n_inputs, n_outputs, device):
        super(NoisyLayer, self).__init__()
        self.n_inputs = n_inputs
        self.n_outputs = n_outputs
        self.device = device

        self.mu_w = nn.Parameter(torch.Tensor(self.n_outputs, self.n_inputs))
        self.sigma_w = nn.Parameter(torch.Tensor(self.n_outputs, self.n_inputs))
        self.register_buffer('weight_epsilon', torch.FloatTensor(self.n_outputs, self.n_inputs))

        self.mu_b = nn.Parameter(torch.Tensor(self.n_outputs))
        self.sigma_b = nn.Parameter(torch.Tensor(self.n_outputs))
        self.register_buffer('bias_epsilon', torch.FloatTensor(self.n_outputs))

        self.mu_w.data.uniform_(-1 / math.sqrt(self.n_inputs), 1 / math.sqrt(self.n_inputs))
        self.sigma_w.data.fill_(0.1 / math.sqrt(self.n_inputs))

        self.mu_b.data.uniform_(-1 / math.sqrt(self.n_inputs), 1 / math.sqrt(self.n_inputs))
        self.sigma_b.data.fill_(0.1 / math.sqrt(self.n_outputs))

        self.reset_noise()

    def forward(self, inputs):
        x = inputs
        weights = self.mu_w + self.sigma_w * self.weight_epsilon
        biases = self.mu_b + self.sigma_b * self.bias_epsilon
        x = F.linear(x, weights, biases)
        return x

    @staticmethod
    def f(x):
        return torch.sign(x) * torch.sqrt(torch.abs(x))

    def reset_noise(self):
        epsilon_i = self.f(torch.randn(self.n_inputs, device=self.device))
        epsilon_j = self.f(torch.randn(self.n_outputs, device=self.device))
        self.weight_epsilon.copy_(epsilon_j.ger(epsilon_i))
        self.bias_epsilon.copy_(epsilon_j)

Agent

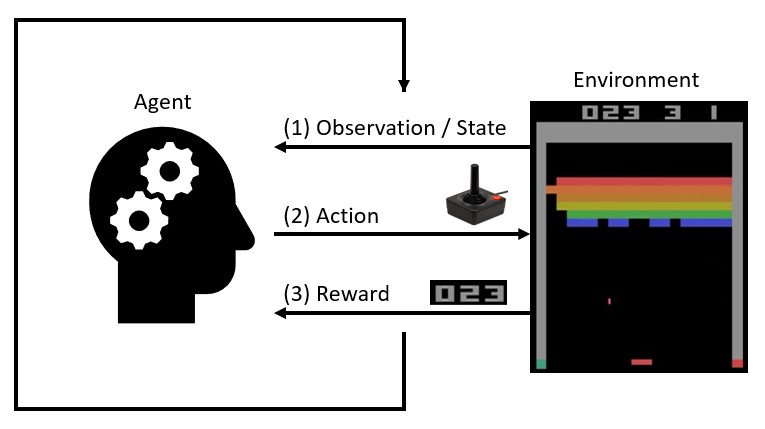
class Agent:
    def __init__(self, **config):
        self.config = config
        self.n_actions = self.config["n_actions"]
        self.state_shape = self.config["state_shape"]
        self.batch_size = self.config["batch_size"]
        self.gamma = self.config["gamma"]
        self.initial_mem_size_to_train = self.config["initial_mem_size_to_train"]
        torch.manual_seed(self.config["seed"])

        if torch.cuda.is_available():
            torch.backends.cudnn.deterministic = True
            torch.backends.cudnn.benchmark = False
            torch.cuda.empty_cache()
            torch.cuda.manual_seed(self.config["seed"])
            torch.cuda.manual_seed_all(self.config["seed"])
            self.device = torch.device("cuda")
        else:
            self.device = torch.device("cpu")

        self.memory = ReplayMemory(self.config["mem_size"], self.config["alpha"], self.config["seed"])
        self.v_min = self.config["v_min"]
        self.v_max = self.config["v_max"]
        self.n_atoms = self.config["n_atoms"]
        self.support = torch.linspace(self.v_min, self.v_max, self.n_atoms).to(self.device)
        self.delta_z = (self.v_max - self.v_min) / (self.n_atoms - 1)
        self.offset = torch.linspace(0, (self.batch_size - 1) * self.n_atoms, self.batch_size).long() \
            .unsqueeze(1).expand(self.batch_size, self.n_atoms).to(self.device)

        self.n_step = self.config["n_step"]
        self.n_step_buffer = deque(maxlen=self.n_step)

        self.online_model = Model(self.state_shape, self.n_actions,
                                  self.n_atoms, self.support, self.device).to(self.device)
        self.target_model = Model(self.state_shape, self.n_actions,
                                  self.n_atoms, self.support, self.device).to(self.device)
        self.hard_update_target_network()

        self.optimizer = optim.Adam(self.online_model.parameters(), lr=self.config["lr"], eps=self.config["adam_eps"])

    def save(self, save_path, beta, episode=0):
        model = {'online': self.online_model.state_dict(), 'beta': beta, 'min_episode': episode}
        torch.save(model, save_path)

    def load(self, load_path):
        checkpoint = torch.load(load_path)
        self.online_model.load_state_dict(checkpoint['online'])
        self.hard_update_target_network()
        params["beta"] = checkpoint['beta']
        self.min_episode = 0

    def plot_and_save(self,
                      episode,
                      episode_reward,
                      episode_loss,
                      episode_g_norm,
                      step,
                      beta,
                      episode_len,
                      show_result=False):
        
        if is_ipython:
            if not show_result:
                display.display(plt.gcf())
                display.clear_output(wait=True)
            else:
                display.display(plt.gcf())
        
        self.rewards.append(episode_reward)
        
        if len(self.rewards) > self.config["save_n_rewards"]:
            self.rewards.pop(0)
            self.avg_rewards.pop(0)

        if len(self.rewards) > self.config["avg_window"]:
            self.avg_rewards.append(np.mean(self.rewards[-self.config["avg_window"]:]))
        else:
            self.avg_rewards.append(0)

        print(f'Episode: {episode}/{self.config["max_steps"]} ' \
              f'| Step: {step} ' \
              f'| Beta: {beta}' \
              f'| Episode reward: {episode_reward} ' \
              f'| Episode loss: {episode_loss}' \
              f'| Episode G-Norm: {episode_g_norm}' \
              f'| Episode Len: {episode_len}'
        )

        plt.figure(1)
        if show_result:
            plt.title('Result')
        else:
            plt.clf()
            plt.title('Training...')
        plt.xlabel('Episode')
        plt.ylabel('Reward')

        x_axis = range(max(1,episode-self.config["save_n_rewards"]+1),episode+1)
        plt.plot(x_axis, self.rewards)
        plt.plot(x_axis, self.avg_rewards)

        plt.pause(0.001)  # pause for plt update

        if episode_reward >= self.best_reward:
            self.best_reward = episode_reward
            self.save(f'atari_trained_online_net_ep_{episode}_{episode_reward}.dat', beta, episode)
        elif self.avg_rewards[-1] > self.best_avg_rewards:
            self.best_avg_rewards = self.avg_rewards[-1]
            self.save(f'atari_trained_online_net_avg_{episode}_{self.avg_rewards[-1]}.dat', beta, episode)

        if show_result:
            self.save('atari_trained_online_net.dat', beta, episode)

    def choose_action(self, state):
        state = np.expand_dims(state, axis=0)
        state = torch.from_numpy(state).byte().to(self.device)
        with torch.no_grad():
            self.online_model.reset()
            action = self.online_model.get_q_value(state).argmax(-1)
        return action.item()

    def store(self, state, action, reward, next_state, done):
        """Save I/O s to store them in RAM and not to push pressure on GPU RAM """
        assert state.dtype == "uint8"
        assert next_state.dtype == "uint8"
        assert isinstance(reward, int)
        assert isinstance(done, bool)

        self.n_step_buffer.append((state, action, reward, next_state, done))
        if len(self.n_step_buffer) < self.n_step:
            return

        reward, next_state, done = self.get_n_step_returns()
        state, action, *_ = self.n_step_buffer.popleft()

        self.memory.add(state, np.uint8(action), reward, next_state, done)

    def soft_update_target_network(self, tau):
        for target_param, local_param in zip(self.target_model.parameters(), self.online_model.parameters()):
            target_param.data.copy_(tau * local_param.data + (1.0 - tau) * target_param.data)
        # self.target_model.train()
        for param in self.target_model.parameters():
            param.requires_grad = False

    def hard_update_target_network(self):
        self.target_model.load_state_dict(self.online_model.state_dict())
        # self.target_model.train()
        for param in self.target_model.parameters():
            param.requires_grad = False

    def unpack_batch(self, batch):
        batch = self.config["transition"](*zip(*batch))

        states = torch.from_numpy(np.stack(batch.state)).to(self.device)
        actions = torch.from_numpy(np.stack(batch.action)).to(self.device).view((-1, 1))
        rewards = torch.from_numpy(np.stack(batch.reward)).to(self.device).view((-1, 1))
        next_states = torch.from_numpy(np.stack(batch.next_state)).to(self.device)
        dones = torch.from_numpy(np.stack(batch.done)).to(self.device).view((-1, 1))
        return states, actions, rewards, next_states, dones

    def train(self, beta):
        if len(self.memory) < self.initial_mem_size_to_train:
            return 0, 0  # as no loss
        batch, weights, indices = self.memory.sample(self.batch_size, beta)
        states, actions, rewards, next_states, dones = self.unpack_batch(batch)
        weights = torch.from_numpy(weights).float().to(self.device)

        with torch.no_grad():
            self.online_model.reset()
            self.target_model.reset()
            q_eval_next = self.online_model.get_q_value(next_states)
            selected_actions = torch.argmax(q_eval_next, dim=-1)
            q_next = self.target_model(next_states)[range(self.batch_size), selected_actions]

            projected_atoms = rewards + (self.gamma ** self.n_step) * self.support * (~dones)
            projected_atoms = projected_atoms.clamp(min=self.v_min, max=self.v_max)

            b = (projected_atoms - self.v_min) / self.delta_z
            lower_bound = b.floor().long()
            upper_bound = b.ceil().long()
            lower_bound[(upper_bound > 0) * (lower_bound == upper_bound)] -= 1
            upper_bound[(lower_bound < (self.n_atoms - 1)) * (lower_bound == upper_bound)] += 1

            projected_dist = torch.zeros(q_next.size(), dtype=torch.float64).to(self.device)
            projected_dist.view(-1).index_add_(0, (lower_bound + self.offset).view(-1),
                                               (q_next * (upper_bound.float() - b)).view(-1))
            projected_dist.view(-1).index_add_(0, (upper_bound + self.offset).view(-1),
                                               (q_next * (b - lower_bound.float())).view(-1))

        eval_dist = self.online_model(states)[range(self.batch_size), actions.squeeze().long()]
        dqn_loss = -(projected_dist * torch.log(eval_dist + 1e-6)).sum(-1)
        td_error = dqn_loss.abs() + 1e-6
        self.memory.update_priorities(indices, td_error.detach().cpu().numpy())
        dqn_loss = (dqn_loss * weights).mean()

        self.optimizer.zero_grad()
        dqn_loss.backward()
        grad_norm = torch.nn.utils.clip_grad_norm_(self.online_model.parameters(), self.config["clip_grad_norm"])
        self.optimizer.step()

        return dqn_loss.item(), grad_norm.item()

    def convert_state(self, state):
        # Return imput image as a tensor
        # return torch.from_numpy((np.array(state)/255).astype(np.float32)).unsqueeze(0).to(device)
        # return (np.array(state)/255).astype(np.float32)
        return state

    def run(self):
        self.best_reward = 0
        self.best_avg_rewards = 0
        self.rewards = []
        self.avg_rewards = []

        if not params["train_from_scratch"]:
            print("Keep training from previous run.")
        else:
            self.min_episode = 0
            print("Train from scratch.")

        if params["do_train"]:
            sign = lambda x: bool(x > 0) - bool(x < 0)
            state = np.zeros(shape=params["state_shape"], dtype=np.uint8)
            obs, info = env.reset()
            self.lives = info['lives']
            state = self.convert_state(obs)
            episode_reward = 0
            episode_len = 0
            episode_loss , episode_g_norm = 0, 0
            beta = params["beta"]

            episode = self.min_episode + 1
            for step in range(1, params["max_steps"] + 1):
                episode_len += 1
                action = agent.choose_action(state)
                next_obs, reward, terminated, truncated, info = env.step(action)
                # Click FIRE if definced also when losing live
                if game_params['FIRE_TO_START'] and info['lives'] < self.lives:
                    self.lives = info['lives']
                    next_obs, reward, terminated, truncated, _ = env.step(1)
                done = terminated or truncated
                # For pacman, optimize eating fruits and not other rewards to focus on finish the game
                if game_params['OPT_FRUITS']:
                    #if reward == 0: reward = -1 # Penalize no score to avoid staying at one place and do nothing
                    if info['lives'] < self.lives: reward = -100  # penalize losing life
                    if reward > 50: reward = 0  # Reward only on eating fruits and vitamins
                    if done: reward = info['lives'] * 100 # Add reward for every life esist
                    self.lives = info['lives']
                next_state = self.convert_state(next_obs)
                r = sign(reward)
                agent.store(state, action, r, next_state, done)
                episode_reward += reward

                if step % params["train_period"] == 0:
                    beta = min(1.0, params["beta"] + step * (1.0 - params["beta"]) / params["final_annealing_beta_steps"])
                    loss, g_norm = agent.train(beta)
                else:
                    loss, g_norm = 0, 0
                episode_loss += loss
                episode_g_norm += g_norm

                if step % params["hard_update_freq"] == 0:
                    agent.hard_update_target_network()

                # env.render()
                state = next_state

                if episode_len == params["max_frames_per_episode"]:
                    done = True

                if done:
                    self.plot_and_save(episode,
                                       episode_reward,
                                       episode_loss / episode_len * params["train_period"],
                                       episode_g_norm / episode_len * params["train_period"],
                                       step,
                                       beta,
                                       episode_len,
                                       False)
                    episode += 1
                    obs, info = env.reset()
                    self.lives = info['lives']
                    state = self.convert_state(obs)
                    episode_reward = 0
                    episode_len = 0
                    episode_loss = 0
                    episode_g_norm = 0

            # save the model
            self.plot_and_save(episode,
                            episode_reward,
                            episode_loss / episode_len * params["train_period"],
                            episode_g_norm / episode_len * params["train_period"],
                            step,
                            beta,
                            episode_len,
                            show_result=True)

    def ready_to_play(self):
        self.online_model.eval()

    def get_n_step_returns(self):
        reward, next_state, done = self.n_step_buffer[-1][-3:]

        for transition in reversed(list(self.n_step_buffer)[:-1]):
            r, n_s, d = transition[-3:]

            reward = r + self.gamma * reward * (1 - d)
            next_state, done = (n_s, d) if d else (next_state, done)

        return reward, next_state, done

Run

params["n_actions"] = env.action_space.n
params["transition"] = namedtuple('transition', ('state', 'action', 'reward', 'next_state', 'done'))
params["train_from_scratch"] = True # Set to False for pre-loading trained policy
agent = Agent(**params)
# agent.load('...') # Load pre trained policy
agent.run()

Play by policy

params["n_actions"] = env.action_space.n
agent = Agent(**params)
# agent.load('...')  # Load pre-trained policy
agent.ready_to_play()

def play_once():
    state, info = env.reset()
    lives = info['lives']
    env_results = []
    done = False
    sum_rewards = 0
    while (not done):
        state = agent.convert_state(state)
        action = agent.choose_action(state)
        state, reward, terminated, truncated, info = env.step(action)
        if game_params['FIRE_TO_START'] and info['lives'] < lives:
            lives = info['lives']
            state, reward, terminated, truncated, info = env.step(1)
        done = terminated or truncated
        sum_rewards += reward
        env_results.append(env.render())
    return sum_rewards, env_results
        
i=0
rewards = []
max_data = {'max_reward':0, 'max_reward_render':[], 'max_steps':0, 'max_steps_render':[], 'max_lives':-1, 'max_lives_render':[]}
while i<1000:
    i+=1
    reward, env_results, lives = play_once()
    rewards.append(reward)
    steps = len(env_results)
    if reward > max_data['max_reward']:
        max_data['max_reward'] = reward
        max_data['max_reward_render'] = env_results
    if steps > max_data['max_steps']:
        max_data['max_steps'] = steps
        max_data['max_steps_render'] = env_results
    if lives > max_data['max_lives']:
        max_data['max_lives'] = lives
        max_data['max_lives_render'] = env_results
    display.clear_output(wait=True)
    print(f"Play {i}, Reward {reward}, Steps {steps}, Max reward {max_data['max_reward']}, Max steps {max_data['max_steps']}, max_lives: {max_data['max_lives']}")
    #if reward >= 1700: break
print(f"Max reward: {max_data['max_reward']}, Max steps: {max_data['max_steps']}, Max lives: {max_data['max_lives']}")

num_plays = len(rewards)
avg_reward = (np.mean(rewards))
max_reward = np.max(rewards)
min_reward = np.min(rewards)
plt.figure()
plt.title(f'Play results. Avg: {avg_reward}, Max: {max_reward}, Min: {min_reward} ')
plt.xlabel('Play')
plt.ylabel('Reward')
plt.plot(range(1,num_plays+1), rewards, color='lightgray')
plt.plot(range(1,num_plays+1), [avg_reward]*num_plays, color='royalblue', linestyle='dashed')
plt.plot(np.argmax(rewards)+1, max_reward, color='indianred', marker='o')
plt.plot(np.argmin(rewards)+1, min_reward, color='goldenrod', marker='o')
plt.grid()

env_results = max_data['max_reward_render']
imageio.mimsave('play-policy.mp4', [frame for frame in env_results], fps=20)

video_widget = ipywidgets.Video.from_file('play-policy.mp4', width=400, autoplay=False, loop=False)
video_widget.add_class('video')
display.display(video_widget)

Play Ramdom

state, info = env.reset()
env_results = []
for i in range(500):
    random_action = env.action_space.sample()
    state, reward, terminated, truncated, info = env.step(random_action)
    done = terminated or truncated
    env_results.append(env.render())
    if done: break
        
imageio.mimsave('play-random.mp4', [frame for frame in env_results], fps=20)

video_widget = ipywidgets.Video.from_file('play-random.mp4', width=400, autoplay=False, loop=False)
video_widget.add_class('video')
display.display(video_widget)